1. General pursuit of nonlinearity

Press the button 'Toggle code' below to toggle code on and off for entire this presentation.

from IPython.display import display
from IPython.display import HTML
import IPython.core.display as di # Example: di.display_html('<h3>%s:</h3>' % str, raw=True)

# This line will hide code by default when the notebook is eåxported as HTML
di.display_html('<script>jQuery(function() {if (jQuery("body.notebook_app").length == 0) { jQuery(".input_area").toggle(); jQuery(".prompt").toggle();}});</script>', raw=True)

# This line will add a button to toggle visibility of code blocks, for use with the HTML export version
di.display_html('''<button onclick="jQuery('.input_area').toggle(); jQuery('.prompt').toggle();">Toggle code</button>''', raw=True)

Toggle code

• We have seen how we can inject nonlinear functions into supervised/unsupervised

• In general we cannot determine what sort of nonliearity to use for a given dataset

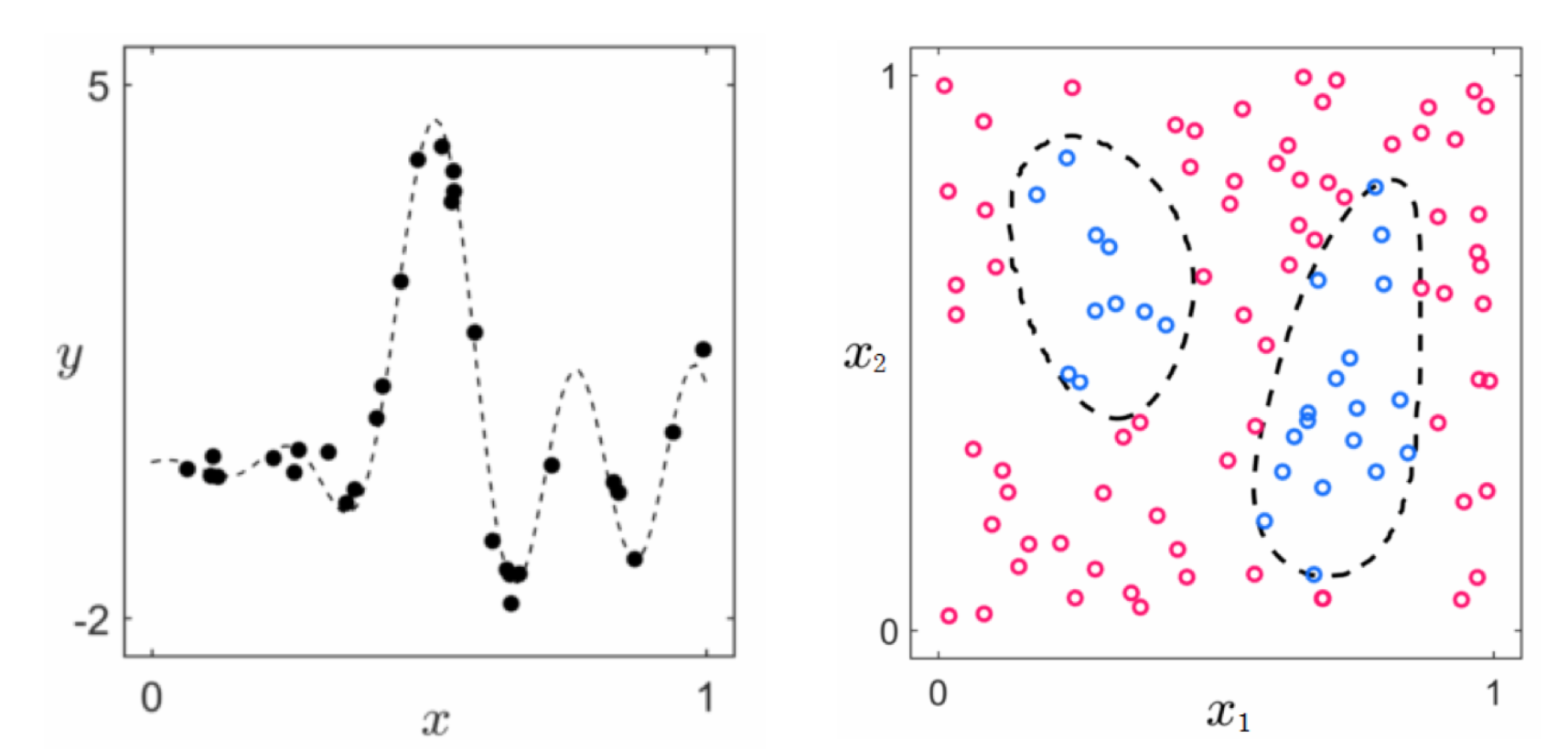
• So we try various combinations of different generic nonlinear functions, and see which combination works best

• We need to be organized and discipline in this search

• Simply taking random combinations of various functions does not allow for effecient computation or fine-tuning of nonlinearity

• Conversely if we retrict ourselves to using a set of related functions we can better manage, optimize, and perform the task

Example 1. A combination of very different functions is difficult to use

• Suppose we have a regression dataset where we cannot guess (via visualization or intuition) a good nonlinearity

• We use a familiar toy data below to simulate our task of searching over various combinations of nonlinear functions to find a fitting nonlinear representation for the data

# create instance of linear regression demo, used below and in the next examples
csvname =  datapath + 'noisy_sin_sample.csv'
demo1 = nonlib.demos_part_2.Visualizer(csvname)
demo1.show_pts()

• Say we limit ourselves to trying linear combinations of the following three functions

\begin{equation} f_1(x) = x ~~~~~~~~~~~~~~ f_2(x) = x^2 ~~~~~~~~~~~~~~ f_3(x) = \text{sinc}(10x) \end{equation}

# plot our features
demo1.plot_feats(version = 1)

• We first try

\begin{equation} \text{model}(x,\mathbf{w}) = w_0 + w_1f_1(x) \end{equation}

• then

\begin{equation} \text{model}(x,\mathbf{w}) = w_0 + w_1\,f_1(x) + w_2\,f_2(x) \end{equation}

• and finally

\begin{equation} \text{model}(x,\mathbf{w}) = w_0 + w_1\,f_1(x) + w_2\,f_2(x) + w_3\,f_3(x) \end{equation}

# show first round of fits
demo1.show_fits(version = 1)

• Here the third function is wildly different than the first two, we are unable to control gradual change in nonlinearity

• Now lets try same experiment but with all three functions related --> polynomials

\begin{equation} f_1(x) = x ~~~~~~~~~~~~~~ f_2(x) = x^2 ~~~~~~~~~~~~~~ f_3(x) = x^3 \end{equation}

# plot our features
demo1.plot_feats(version = 2)

# show first round of fits
demo1.show_fits(version = 2)

• We get a better fit of course, but the change in nonlinearity is more gradual, predictable, and controllable

The three standard species of functions used for prediction

• We could try adding various random functions for our nonlinear predictor e.g.,

\begin{equation} \text{model}(x,\mathbf{w}) = w_0 + w_1\text{tanh}\left(w_2 + w_3x\right) + w_4e^{w_5x} + w_6x^{10} + \cdots \end{equation}

• But to make computationally effecient search methods we need to be more organized than this

• Hence in practice we typically stick to combining functions from a single species - or collection of similar behaving functions

• We use $B$ functions from such a species, making a model function of the form

\begin{equation} \text{model}(x,\mathbf{w}) = w_0 + w_1\,f_1(x) + w_2\,f_2(x) + w_3\,f_3(x) + \cdots + w_B\,f_B(x) \end{equation}

• By adding together such functions we can create any sort of non-linearity we want, easier to control and optimize

• At a high level: three main types of species used in practice - kernels, neural networks, and trees

• Inside each catalog there are many sub-species, here we introduce each species via a simple but common example from each

• We will then circle back to discuss more complex sub-species of neural networks

1. Kernels

• Basic example: polynomials

\begin{equation} f_1(x) = x^1, ~~ f_2(x) = x^2, ~~ f_3(x) = x^3, ~~ f_4(x) = x^4, ... \end{equation}

# import Draw_Bases class for visualizing various basis element types
demo = nonlib.DrawBases.Visualizer()

# plot the first 4 elements of the polynomial basis
demo.show_1d_poly()

demo = nonlib.regression_basis_single.Visualizer()
csvname =  datapath + 'noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_single_fit(basis='poly',num_units = [v for v in range(1,15)])

• For two inputs - $x_1$ and $x_2$ - the catalog of polynomial elements looks like

\begin{equation} f_1(x_1,x_2) = x_1, ~~ f_2(x_1,x_2) = x_2^2, ~~ f(x_1,x_2) = x_1x_2^3, ~~ f(x_1,x_2) = x_1^4x_2^6,... \end{equation}

• In general a degree $D$ element takes the form

\begin{equation} f_m(x_1,x_2) = x_1^px_2^q \end{equation}

where where $p$ and $q$ are nonnegative integers and $p + q \leq D$

demo.show_2d_poly()

demo = nonlib.regression_basis_comparison_3d.Visualizer()
csvname =  datapath + '3d_noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_single_fits(num_elements =  [v for v in range(1,10)] ,view = [20,110],basis = 'poly')

• Can be defined likewise for general $N$ input dimension

• General attributes of kernel bases:
  • classic examples also include: Fourier and cosine bases, radial basis functions
  • each element has a fixed shape (no internal parameters), elements are ordered from simple to complex
  • always leads to convex cost functions for regression / classification
  • great for medium sized problems, but many varieties have serious scaling issues when $N$ and $P$ are large
  • often used with support vector machines (for historical reasons)

2. Neural networks

• Basic example: single hidden layer network with tanh activation

\begin{equation} f_1(x) = \text{tanh}\left(w_{1,0} + w_{1,1}x\right), ~~ f_2(x) = \text{tanh}\left(w_{2,0} + w_{2,1}x\right), ~~ f_3(x) = \text{tanh}\left(w_{3,0} + w_{3,1}x\right), ~~ f_4(x) = \text{tanh}\left(w_{4,0} + w_{4,1}x\right), ... \end{equation}

• Internal parameters make each function flexible

• e.g., take $f_1$ with various internal parameter settings

# import Draw_Bases class for visualizing various basis element types
demo = nonlib.DrawBases.Visualizer()

# plot the first 4 elements of the polynomial basis
demo.show_1d_net(num_layers = 1,activation = 'tanh')

• Basic example: single hidden layer network with relu activation

\begin{equation} f_1(x) = \text{max}\left(0,w_{1,0} + w_{1,1}x\right), ~~ f_2(x) = \text{max}\left(0,w_{2,0} + w_{2,1}x\right), ~~ f_3(x) = \text{max}\left(0,w_{3,0} + w_{3,1}x\right), ~~ f_4(x) = \text{max}\left(0,w_{4,0} + w_{4,1}x\right), ... \end{equation}

• Internal parameters make each function flexible

# import Draw_Bases class for visualizing various basis element types
demo = nonlib.DrawBases.Visualizer()

# plot the first 4 elements of the polynomial basis
demo.show_1d_net(num_layers = 1,activation = 'relu')

demo = nonlib.regression_basis_single.Visualizer()
csvname = datapath + 'noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_single_fit(basis='tanh',num_units = [v for v in range(1,15)])

• For two inputs - $x_1$ and $x_2$ - the catalog of single layer functions with relu activation

\begin{equation} f_1(x) = \text{tanh}\left(w_{1,0} + w_{1,1}x_1 + w_{1,2}x_2\right), ~~ f_2(x) = \text{tanh}\left(w_{2,0} + w_{2,1}x_1 + w_{2,2}x_2\right) ... \end{equation}

• or likewise

\begin{equation} f_1(x) = \text{max}\left(0,w_{1,0} + w_{1,1}x_1 + w_{1,2}x_2\right), ~~ f_2(x) = \text{max}\left(0,w_{2,0} + w_{2,1}x_1 + w_{2,2}x_2\right) ... \end{equation}

demo = nonlib.regression_basis_comparison_3d.Visualizer()
csvname = datapath + '3d_noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_single_fits(num_units =  [v for v in range(1,12)] ,view = [20,110],basis = 'net')

• Generalizes to $N$ dimensional input

• General attributes of neural network bases:
  • elements are of the same general type, each has adjustable shape (with internal parameters)
  • leads to non-convex cost functions for regression / classification
  • especially great for large high dimensional input problems
  • often used with logistic regression (for historical reasons)

3. Trees

• Basic example: depth-1 tree, also known as a stump

\begin{equation} f_1(x) = \begin{cases} x < V_1 \,\,\,\,\, a_1 \\ x \geq V_1 \,\,\,\,\, b_1 \end{cases} ~~~~~~~~ f_2(x) = \begin{cases} x < V_2 \,\,\,\,\, a_2 \\ x \geq V_2 \,\,\,\,\, b_2 \end{cases} ~~ \cdots \end{equation}

• Vocab: for $f_j$ the value $V_j$ called a split point, $a_j$ and $b_j$ called levels

# import Draw_Bases class for visualizing various basis element types
demo = nonlib.DrawBases.Visualizer()

# plot the first 4 elements of the polynomial basis
demo.show_1d_tree(depth = 1)

• Split points and levels set directly using data, not internal parameters

• e.g., a split point placed between two inputs, left / right level set to average of output to the left / right

demo = nonlib.stump_visualizer_2d.Visualizer()
csvname = datapath + 'noisy_sin_raised.csv'
demo.load_data(csvname)
demo.browse_stumps()

demo = nonlib.regression_basis_single.Visualizer()
csvname = datapath + 'noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_single_fit(basis='tree',num_elements = [v for v in range(1,10)])

demo = nonlib.regression_basis_comparison_3d.Visualizer()
csvname = datapath + '3d_noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_single_fits(num_elements =  [v for v in range(1,20)] ,view = [20,110],basis = 'tree')

• Generalizes to $N$ dimensional input (split points / levels in each individual dimension)

• General attributes of tree bases:
  • each element is adjustable, with internal parameters pre-set greedily to data
  • leads to convex cost functions for regression / classification, trained via boosting (greedy coordinate descent)
  • great for large sparse datasets

How many elements to choose?

• The more elements we use the better we fit our data (provided we optimize correctly)

• This is good in theory, but not in practice

• In theory -with infinite clean data and ininite computation - the more elements (of any basis) --> better fit / separation

• In fact: in such an instance all three catalogues equal, and can perfectly represent / separate

demo = nonlib.regression_basis_comparison_2d.Visualizer()
csvname = datapath + 'sin_function.csv'
demo.load_data(csvname)
demo.brows_fits(num_elements = [v for v in range(1,50,1)])

• With real data however more elements $\neq$ better fit

demo = nonlib.regression_basis_comparison_2d.Visualizer()
csvname = datapath + 'noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_fits(num_elements = [v for v in range(1,25)])

• Nothing has 'gone wrong' here - we just do not know ahead of time how many elements is 'too little' and how many is 'too much' (in terms of nonlinearity)

• i.e., error on training set always goes down as we add elements (provided we optimize correctly)

demo = nonlib.regression_basis_single.Visualizer()
csvname = datapath + 'noisy_sin_sample.csv'
demo.load_data(csvname)
demo.brows_single_fit(basis='poly',num_elements = [v for v in range(1,25)])

• When fit is not nonlinear enough / we use too few basis features --> call this underfitting

• When fit is too nonlinear / we use too many basis features --> call this overfitting

• The way of finding best combination of elements to use called cross-validation