6.4 Gradient descent

Press the button 'Toggle code' below to toggle code on and off for entire this presentation.

from IPython.display import display
from IPython.display import HTML
import IPython.core.display as di # Example: di.display_html('<h3>%s:</h3>' % str, raw=True)

# This line will hide code by default when the notebook is exported as HTML
di.display_html('<script>jQuery(function() {if (jQuery("body.notebook_app").length == 0) { jQuery(".input_area").toggle(); jQuery(".prompt").toggle();}});</script>', raw=True)

# This line will add a button to toggle visibility of code blocks, for use with the HTML export version
di.display_html('''<button onclick="jQuery('.input_area').toggle(); jQuery('.prompt').toggle();">Toggle code</button>''', raw=True)

Toggle code

6.4.1 The gradient descent algorithm

A local optimization method is one where we aim to find minima of a given function by beginning at some point $\mathbf{w}^0$ and taking number of steps $\mathbf{w}^1, \mathbf{w}^2, \mathbf{w}^3,...,\mathbf{w}^{K}$ of the generic form

\begin{equation} \mathbf{w}^{\,k} = \mathbf{w}^{\,k-1} + \alpha \mathbf{d}^{\,k}. \end{equation}

where $\mathbf{d}^{\,k}$ are direction vectors (which ideally are descent directions that lead us to lower and lower parts of a function) and $\alpha$ is called the steplength parameter.

We could very naturally ask what a local method employing the negative gradient direction at each step might look like, and how it might behave - i.e., setting $\mathbf{d}^{k} = -\nabla g\left(\mathbf{w}^{k-1}\right)$ in the above formula. Such a sequence of steps would then take the form

\begin{equation} \mathbf{w}^{\,k} = \mathbf{w}^{\,k-1} - \alpha \nabla g\left(\mathbf{w}^{k-1}\right) \end{equation}

Indeed this is precisely the gradient descent algorithm. It is it called gradient descent - in employing the (negative) gradient as our descent direction - we are repeatedly descending in the (negative) gradient direction at each step.

Figure 1: A figurative drawing of the gradient descent algorithm. The first order Taylor series approximation - and the *negative gradient* of the function in particular - provides an excellent and easily computed descent direction at each step of this local optimization method (here a number of Taylor series approximations are shown in green, and evaluations by the function and linear approximations are shown as red dots and crosses respectively). Employing these directions at each step the *gradient descent algorithm* can be used to properly minimize generic functions. Moreover, unlike the random local search algorithm, gradient descent scales very well with input dimension since the descent direction of a hyperplane is much more easily computed in high dimensions.

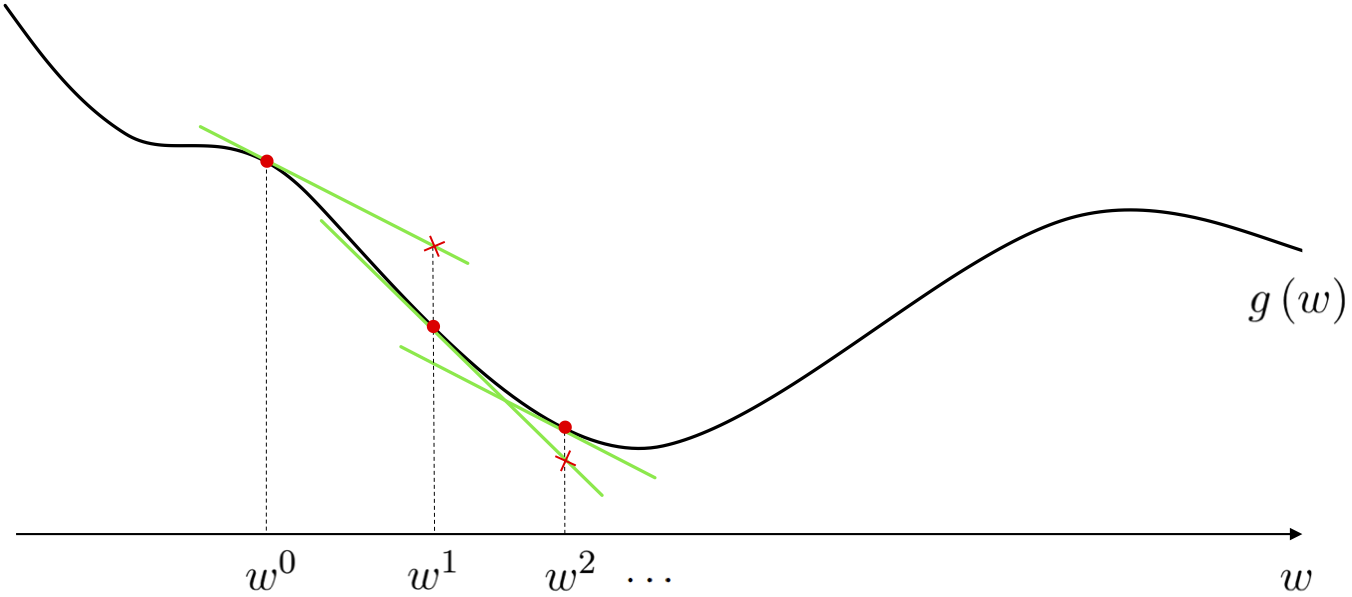
• Appreciate the power of this descent direction - which is almost literally given to us - over the zero-order methods. There we had to search to find a descent direction, here calculus provides us not only with a descent direction (without search), but an excellent one to boot.

• This has made gradient descent the most popular optimization algorithm used in machine learning / deep learning today.

• Additionally, we can very easily compute the gradient of almost any generic function of interest using a gradient calculator known as an Automatic Differentiator. So in practice we need not even have to worry about computing the form of a function's gradient 'by hand'.

The gradient descent algorithm

---

1:   input: function $g$, steplength $\alpha$, maximum number of steps $K$, and initial point $\mathbf{w}^0$
2:   for $\,\,k = 1...K$
3:           $\mathbf{w}^k = \mathbf{w}^{k-1} - \alpha \nabla g\left(\mathbf{w}^{k-1}\right)$
4:  output: history of weights $\left\{\mathbf{w}^{k}\right\}_{k=0}^K$ and corresponding function evaluations $\left\{g\left(\mathbf{w}^{k}\right)\right\}_{k=0}^K$

---

# using an automatic differentiator - like the one imported via the statement below - makes coding up gradient descent a breeze
from autograd import value_and_grad 

# gradient descent function - inputs: g (input function), alpha (steplength parameter), max_its (maximum number of iterations), w (initialization)
def gradient_descent(g,alpha_choice,max_its,w):
    # compute the gradient function of our input function - note this is a function too
    # that - when evaluated - returns both the gradient and function evaluations (remember
    # as discussed in Chapter 3 we always ge the function evaluation 'for free' when we use
    # an Automatic Differntiator to evaluate the gradient)
    gradient = value_and_grad(g)

    # run the gradient descent loop
    weight_history = []      # container for weight history
    cost_history = []        # container for corresponding cost function history
    alpha = 0
    for k in range(1,max_its+1):
        # check if diminishing steplength rule used
        if alpha_choice == 'diminishing':
            alpha = 1/float(k)
        else:
            alpha = alpha_choice
        
        # evaluate the gradient, store current weights and cost function value
        cost_eval,grad_eval = gradient(w)
        weight_history.append(w)
        cost_history.append(cost_eval)

        # take gradient descent step
        w = w - alpha*grad_eval
            
    # collect final weights
    weight_history.append(w)
    # compute final cost function value via g itself (since we aren't computing 
    # the gradient at the final step we don't get the final cost function value 
    # via the Automatic Differentiatoor) 
    cost_history.append(g(w))  
    return weight_history,cost_history

6.4.2 General behavior of gradient descent

• Gradient descent converges to stationary points of a function: because we employ the (negative) gradient as our descent direction, the algorithm converges at / nearby stationary points

• Gradient descent makes great progress far from stationary points, but crawls to a halt near them: in addition to the steplength parameter $\alpha$ the magnitude of the gradient controls how far we travel at each step of gradient descent, and this has both positive and negative consequences for performance

• Non-convexity is not an inherent problem for gradient descent, but saddle points are: due to its convergence behavior saddle points pose an inherent problem for gradient descent

• Gradient descent scales well with input dimension: because the gradient can be computed extremely efficiently gradient descent scales very well, computationally speaking, with the size of input dimension

• Just like all local methods, one needs to carefully choose the steplength parameter $\alpha$: like all local optimization methods the steplength parameter $\alpha$ must be set properly in order to provoke timely convergence, with the most popular choices in machine learning / deep learning being the fixed and diminishing steplength rules.

Example 1. Gradient descent converges to stationary points of a function

• We use gradient descent to minimize the polynomial function

\begin{equation} g(w) = \frac{1}{50}\left(w^4 + w^2 + 10w\right). \end{equation}

• In this case the global minimum of this problem - which we could not compute by hand easily - is given explicitly as
  \begin{equation} w = \frac{\sqrt[\leftroot{-2}\uproot{2}3]{\sqrt[\leftroot{-2}\uproot{2}]{2031} - 45}}{6^{\frac{2}{3}}} - \frac{1}{\sqrt[\leftroot{-2}\uproot{2}3]{6\left(\sqrt{2031}-45\right)}} \end{equation}

# what function should we play with?  Defined in the next line.
g = lambda w: 1/float(50)*(w**4 + w**2 + 10*w)   # try other functions too!  Like g = lambda w: np.cos(2*w) , g = lambda w: np.sin(5*w) + 0.1*w**2, g = lambda w: np.cos(5*w)*np.sin(w)

# run gradient descent 
w = 2.5; alpha_choice = 1; max_its = 25;
weight_history,cost_history = gradient_descent(g,alpha_choice,max_its,w)

# animate gradient descent applied to minimizing this function
anime_plotter.gradient_descent(g,weight_history)

Notice, how the slope of the tangent line - which is the magnitude of the derivative - goes to zero as we approach the minimum because here $\nabla g\left(\mathbf{w}^k\right) \approx \mathbf{0}_{N\times 1}$. This makes sense for two reasons:

• if gradient descent does truly reach a minimum point on a function we know - from the first order condition of optimality - that the gradient here must indeed be vanishing.

• we can see from the very form of the gradient descent step that the only way for this algorithm to truly converge - that is for the steps to settle down and stop changing i.e., $\mathbf{w}^{k-1} \approx \mathbf{w}^k$ - is for the gradient to be approximately zero $\nabla g\left(\mathbf{w}^k\right) \approx \mathbf{0}_{N\times 1}$.

• Next we run gradient descent on the multi-input quadratic function $g(w_1,w_2) = w_1^2 + w_2^2 + 2$.

• We take 10 steps each using the steplength $\alpha = 0.1$.

# show run in both three-dimensions and just the input space via the contour plot
static_plotter.two_input_surface_contour_plot(g,weight_history,view = [10,30])

We can visualize the cost function history plot to see the progress of this run (for parameter tuning and debugging purposes). This can be done regardless of the dimension of the function we are minimizing.

# plot the cost function history for a given run
static_plotter.plot_cost_histories([cost_history],start = 0,points = True,labels = ['gradient descent run'])

Example 2. Gradient descent makes great progress far from stationary points, but crawls to a halt near them

# what function should we play with?  Defined in the next line.
g = lambda w: w**4 + 0.1

# run gradient descent 
w = -1.0; max_its = 15; alpha_choice = 0.1;
weight_history,cost_history = gradient_descent(g,alpha_choice,max_its,w)

# make static plot showcasing each step of this run
static_plotter.single_input_plot(g,[weight_history],[cost_history],wmin = -1.1,wmax = 1.1)

In all instances shown above, while the steplength parameter $\alpha$ has been fixed for all iterations, the actual length of each step appears to be changing from step-to-step. There are two reasons for this behavior:

• if we analyze the length of the $k^{th}$ step - i.e., the value $\Vert \mathbf{w}^k - \mathbf{w}^{k-1} \Vert_2$ - we can see that the length of each step is not solely controlled by the steplength parameter $\alpha$

\begin{equation} \Vert \mathbf{w}^k - \mathbf{w}^{k-1} \Vert_2 = \Vert \left(\mathbf{w}^{k-1} - \alpha\nabla g\left(\mathbf{w}^{k-1}\right) \right) - \mathbf{w}^{k-1} \Vert_2 = \alpha \Vert \nabla g\left(\mathbf{w}^{k-1}\right) \Vert_2. \end{equation}

• since the length of each step is proportional to the magnitude of the gradient this means that when that magnitude is large - e.g., at points far away from a stationary point where the gradient / slope(s) of the tangent hyperplane are large - gradient descent takes larger steps. Conversely, when close to a stationary point where the gradient / slopes of the tangent hyperplane are small (and near zero), gradient descent takes small steps.

• The second reason for gradient descent slowing down near stationary points has to do with the geometric nature of many functions: many functions of interest in machine learning / deep learning have minima that lie in long narrow valleys i.e., long flat regions.

• Recall that the (negative) gradient is always perpendicular to the contour of the function it lies on. Because of this the gradient direction tends to zig-zag in long narrow valleys, causing zig-zagging behavior in gradient descent itself.

We illustrate this behavior with an $N = 2$ dimensional quadratic below.

# show run in both three-dimensions and just the input space via the contour plot
static_plotter.two_input_contour_plot(g,weight_history,num_contours = 9,xmin = -1,xmax = 8.5,ymin = -1,ymax = 1,show_original = False)

Another example: the Rosenbrock function which takes the form

\begin{equation} g\left(w_0,w_1\right) = 100\left(w_0 - w_1^2\right)^2 + \left(w_0 - 1\right)^2. \end{equation}

# define function
g = lambda w: 100*(w[1] - w[0]**2)**2 + (w[0] - 1)**2 

# run random search algorithm 
alpha_choice = 0.0001; w = np.array([-2.0,-2.0]); max_its = 2000;
weight_history_1,cost_history_1 = gradient_descent(g,alpha_choice,max_its,w)

# show run in both three-dimensions and just the input space via the contour plot
static_plotter.two_input_contour_plot(g,weight_history_1,num_contours = 9,xmin = -2.5,xmax = 2.5,ymin = -2.25,ymax = 2)

Example 3. Non-convexity is not an inherent problem for gradient descent, but saddle points are

# what function should we play with?  Defined in the next line.
g = lambda w: np.sin(3*w) + 0.1*w**2

# run gradient descent
alpha_choice = 0.05; w = 4.5; max_its = 10;
weight_history_1,cost_history_1 = gradient_descent(g,alpha_choice,max_its,w)

alpha_choice = 0.05; w = -1.5; max_its = 10;
weight_history_2,cost_history_2 = gradient_descent(g,alpha_choice,max_its,w)

# make static plot showcasing each step of this run
static_plotter.single_input_plot(g,[weight_history_1,weight_history_2],[cost_history_1,cost_history_2],wmin = -5,wmax = 5)

We can plot both runs using the cost function history plot which allows us to view the progress of gradient descent (or any local optimization method - see Section 5.4 where they are first introduced) runs regardless of the input dimension of the function we are minimizing.

# plot the cost function history for a given run
static_plotter.plot_cost_histories([cost_history_1,cost_history_2],start = 0,points = True,labels = ['run 1','run 2'])

While non-convexity is itself not a problem, saddle points of a non-convex function do pose a problem to the progress of gradient descent because gradient descent naturally slows down near any stationary point of a function.

g = lambda w: np.maximum(0,(3*w - 2.3)**3 + 1)**2 + np.maximum(0, (-3*w + 0.7)**3 + 1)**2

# run the visualizer for our chosen input function, initial point, and step length alpha
demo = optlib.gradient_descent_demos.visualizer();

# draw function and gradient descent run
demo.draw_2d(g=g, w_inits = [0],steplength = 0.01,max_its = 20,version = 'unnormalized',wmin = 0,wmax = 1.0)

Example 4. Gradient descent scales well with input dimension

Since the gradient immediately supplies us with an excellent descent direction, the gradient descent algorithm scales gracefully with input dimension (unlike zero-order methods).

Example 5. Just like all local methods, one needs to carefully choose the steplength parameter $\alpha$

# what function should we play with?  Defined in the next line., nice setting here is g = cos(2*w), w_init = 0.4, alpha_range = np.linspace(2*10**-4,1,200)
g = lambda w: w**2

# create an instance of the visualizer with this function
demo = optlib.grad_descent_steplength_adjuster_2d.visualizer()

# run the visualizer for our chosen input function, initial point, and step length alpha
w_init = -2.5
steplength_range = np.linspace(10**-5,1.5,150)
max_its = 5
demo.animate_it(w_init = w_init, g = g, steplength_range = steplength_range,max_its = max_its,tracers = 'on',version = 'unnormalized')

It is good practice when implementing gradient descent (employing hand-tuned fixed steplength or diminishing steplength rule) to keep track of the best weights seen thus far in the process (i.e., those providing the lowest function value). This is because the final weights resulting from the run may not in fact provide the lowest value depending on function / steplength parameter setting / etc.

The same concept, this time in 2-d

# what function should we play with?  Defined in the next line., nice setting here is g = cos(2*w), w_init = 0.4, alpha_range = np.linspace(2*10**-4,1,200)
g = lambda w: np.sin(w[0])

# create an instance of the visualizer with this function
demo = optlib.grad_descent_steplength_adjuster_3d.visualizer()

# run the visualizer for our chosen input function, initial point, and step length alpha
w_init = [1,0]; alpha_range = np.linspace(2*10**-4,5,100); max_its = 10; view = [10,120];
demo.animate_it(g = g,w_init = w_init,alpha_range = alpha_range,max_its = max_its,view = view)

Below we illustrate the comparison of a fixed steplength scheme and a the diminishing steplength rule to minimize the function

\begin{equation} g(w) = \left \vert w \right \vert. \end{equation}

Notice that this function has a single global minimum at $w = 0$ and a derivative defined (everywhere but at $w = 0$)

\begin{equation} \frac{\mathrm{d}}{\mathrm{d}w}g(w) = \begin{cases} +1 \,\,\,\,\,\text{if} \,\, w > 0 \\ -1 \,\,\,\,\,\text{if} \,\, w < 0. \end{cases} \end{equation}

which makes the use of any fixed steplength scheme problematic for gradient descent.

• left: fixed steplength rule of $\alpha = 0.5$
• right: diminishing steplength rule $\alpha = \frac{1}{k}$

# what function should we play with?  Defined in the next line.
g = lambda w: np.abs(w)

# run gradient descent
alpha_choice = 0.5; w = 1.75; max_its = 20;
weight_history_1,cost_history_1 = gradient_descent(g,alpha_choice,max_its,w)

alpha_choice = 'diminishing'; w = 1.75; max_its = 20;
weight_history_2,cost_history_2 = gradient_descent(g,alpha_choice,max_its,w)

# make static plot showcasing each step of this run
static_plotter.single_input_plot(g,[weight_history_1,weight_history_2],[cost_history_1,cost_history_2],wmin = -2,wmax = 2,onerun_perplot = True)

• Here a diminishing steplength is absolutely necessary in order to reach a point close to the minimum.
• We can see this even more clearly via the cost function history plot.

# plot the cost function history for a given run
static_plotter.plot_cost_histories([cost_history_1,cost_history_2],start = 0,points = True,labels = [r'$\alpha = 0.5$',r'\alpha = \frac{1}{k}$'])

6.4.3 Convergence behavior and steplength parameter selection

When do we know gradient descent has reached a local minimum? In other words, how do we know when to stop the algorithm?

• Theoretically speaking, we can evaluate the length (or magnitude) of the gradient $\left\Vert \nabla g\left(\mathbf{w}^{\,k-1}\right)\right\Vert_2$. If this value is small then the algorithm has by definition reached a stationary point of the function.

• Practically speaking, halting the procedure after a pre-set number of maximum iterations is a common stopping condition for gradient descent in the machine learning / deep learning community.

What is good number for a maximum iteration count?

• This is typically set manually / heuristically, and is influenced by things like computing resources, knowledge of the particular function being minimized, and - very importantly - the choice of the steplength parameter $\alpha$. Smaller choices for $\alpha$ - while more easily providing descent at each step - frequently require more for the algorithm to achieve significant progress. Conversely if $\alpha$ is set too large gradient descent may bounce around erratically forever never localizing in an adequate solution.

How do we choose the steplength?

• While there are a variety of mathematical tools that can give guidance as to how to set $\alpha$ in general, often in practice in machine learning / deep learning problems the steplength parameter $\alpha$ is determined by trial and error. This often includes running gradient descent a number of times while trying out different fixed $\alpha$ values, or various diminishing steplength schemes, to determine which provides the lowest function value.